英国数学奥林匹克竞赛(British Mathematical Olympiad,BMO)是UKMT系列中最具挑战性的竞赛项目,以往为邀请赛(SMC竞赛前1000位有机会),考察学生的数学综合学术实力。
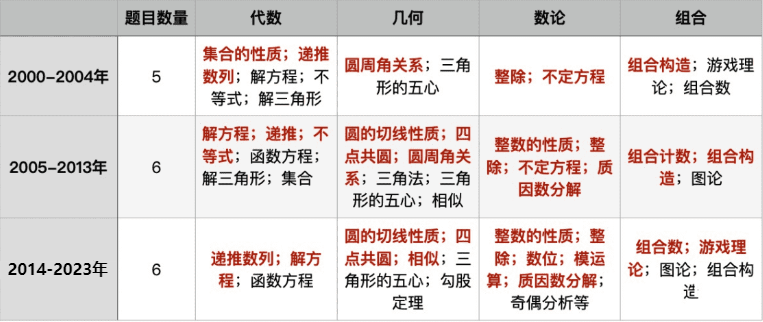
1.2000-2004年数学竞赛题目内容概述:
在代数领域,竞赛题目涉及了集合性质、递推数列、解方程、不等式、解三角形等内容,旨在考察代数知识的掌握和应用能力。这些题目要求参赛者具备对代数概念的深入理解,并能够灵活运用这些概念解决复杂的数学问题。
另一方面,在几何领域,竞赛题目涉及了圆周角关系、三角形的五心等内容,要求参赛者对几何图形性质的深入理解和运用能力。这些题目考察了参赛者对几何概念的掌握程度以及其在解决几何问题时的灵活应用能力。
此外,数论领域的竞赛题目涉及了整除、不定方程等内容,需要参赛者熟练掌握数论知识和灵活运用能力。这些题目旨在考察参赛者对数论原理的理解程度以及其在解决数论问题时的推理能力。
最后,在组合领域,竞赛题目涉及了组合构造、游戏理论、组合数等内容,要求参赛者具备较强的逻辑思维和组合计数能力。这些题目考察了参赛者在处理组合问题时的分析能力和解决问题的灵活性。
2.2005-2013年数学竞赛题目内容概述:
在代数领域,竞赛题目涉及了解方程、递推、不等式、函数方程、解三角形、集合等方面的内容,考察了参赛者较高的代数解题能力。这些题目要求参赛者在代数领域具备较高水平的问题解决能力,并能够灵活运用代数知识解决复杂的数学难题。
另一方面,在几何领域,竞赛题目涉及了圆的切线性质、四点共圆、圆周角关系、三角法、三角形的五心、相似等内容,考察了几何性质的深入理解和运用能力。这些题目要求参赛者对几何性质有着深刻的理解,并能够将几何知识灵活运用于解决复杂的几何问题。
此外,数论领域的竞赛题目涉及了整数的性质、整除、不定方程、质因数分解等内容,要求参赛者具备较强的数论分析和推理能力。这些题目旨在考察参赛者对数论知识的深入理解以及其在解决数论问题时的逻辑推理能力。
最后,在组合领域,竞赛题目涉及了组合计数、组合构造、图论等内容,要求参赛者具备较强的组合计数和图论分析能力。这些题目考察了参赛者在组合问题和图论问题上的分析能力和解决问题的灵活性。
3.2014-2023年数学竞赛题目内容概述:
在代数领域,竞赛题目涉及了递推数列、解方程、函数方程等内容,要求参赛者具备较高的代数分析和解题能力。这些题目考察了参赛者在代数领域的问题解决能力,并能够灵活运用代数知识解决复杂的数学难题。
另一方面,在几何领域,竞赛题目涉及了圆的切线性质、四整数的性质、整点共圆、相似、三除、数位、模运角形的五心、勾股算和质因数分解定理等内容,考察了几何性质和定理的深入理解和运用能力。这些题目要求参赛者对几何性质有着深刻的理解,并能够将几何知识灵活运用于解决复杂的几何问题。
此外,数论领域的竞赛题目涉及了圆的切线性质、四整数的性质、整点共圆、相似、三除、数位、模运角形的五心、勾股算和质因数分解定理等内容,要求参赛者具备较强的数论分析和推理能力。这些题目旨在考察参赛者对数论知识的深入理解以及其在解决数论问题时的逻辑推理能力。
最后,在组合领域,竞赛题目涉及了组合数、游戏理论、图论和组合构造等内容,要求参赛者具备较强的组合计数和图论分析能力。这些题目考察了参赛者在组合问题和图论问题上的分析能力和解决问题的灵活性。
通过在BMO竞赛中取得优异的成绩,学生们不仅可以为未来的升学背景提升注入强有力的支持,还能够向学院招生官员展示他们在数学领域的才华和潜力,为自己的简历增光添彩。 BMO竞赛的题目难度极高,对数学能力和逻辑推理技巧进行了深入的考察,通过在BMO竞赛中获奖,个人的数学学术能力得到了充分的证明。

