| 竞赛介绍 | 晋级路线 | 参赛对象/考试形式 | 考察内容 |
| 奖项设置 | 赛事含金量 | 备考建议 |
一、BMO竞赛介绍
BMO竞赛全称British Mathematical Olympiad(英国数学奥林匹克竞赛),是成立于1996年的United Kingdom Mathematics Trust(UKMT)英国数学基金会组织的旗下针对高年级中学生的竞赛项目,也是UKMT旗下难度最大的竞赛项目。
UKMT是英国规模最大的数学竞赛组织单位,每年邀请近1000位左右拥有数学天赋的11-18周岁学生分不同年龄层的各项竞赛,考察学生的数学综合学术实力,是英国最具影响力的数学竞赛,也是英国知名度最高的数学竞赛。其中SMC和BMO是参加最多,难度较大,含金量较高的竞赛。

二、晋级路线
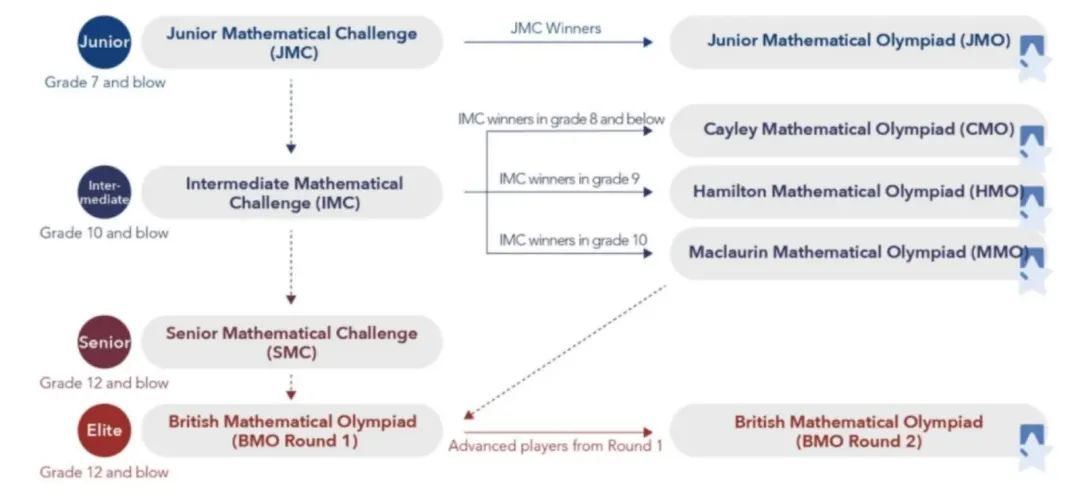
三、BMO参赛对象和考试形式
参赛对象:在校高中生
考试形式:考试以英文形式进行,每场考试3.5小时,每题10分,需要完全化简的答案以及完整的解答过程(部分过程正确也将获得一定的分数),每题10分,Round 1需要完成6道简答题,Round 2需要完成4道简答题。
四、BMO竞赛考察内容
BMO的两轮比赛都是简答题,整体考察6大方面的内容:Geometry几何学、Trigonometry三角学、Functional Equations函数方程、Algebra代数、Number Theory数论以及Combinatorics组合数学。
- Geometry几何学方面:
BMO1中与圆定律相关的内容,例如交错弧定理(Alternate Segment Theorem),是比较重要的。而在BMO2中,除了需要掌握基础的结构认知外,还需要具备一定的几何想象力,比如三角形的4个中心点:外心(circumcentre)、垂心(orthocentre)、内心(incentre)和重心(centroid),以及三角形面积计算的海伦公式(Heron's formula)。
- Trigonometry三角学:
比如Cosine Rule对余弦规则和Sine Rule全部正弦规则等,知道的越多,越有帮助;
- Functional Equations函数方程:
要学会灵活应用替换;
- Algebra代数方面:
对于二次方程(quadratics)以及因式定理(Factor Theorem),需要有深入的理解。此外,在参加BMO2竞赛时,熟练运用柯西-施瓦茨不等式(Cauchy-Schwarz Inequality)可能会非常有用。
- Number Theory数论:
BMO竞赛中难度较高的领域,大多数问题涉及到方程的整数解。在BMO1中,了解模10算术的规则以及它的扩展内容将非常有帮助。而到了BMO2,除了BMO1的内容外,还需要了解费马小定理(Fermat's Little Theorem)等相关概念和定理。
- Combinatorics组合数学方面:
对于BMO1来说,了解二项式系数(Binomial Coefficients)的知识即可。而对于BMO2来说,则至少需要掌握鸽子洞原理(Pigeon-hole Principle),它表明如果有n只鸽子和m个鸽洞,并且n大于m,那么至少有两只鸽子必须在同一个鸽洞里。此外,在计数方法的构建过程中,掌握递归关系的概念会非常有帮助。另外,图论(Graph Theory)的相关内容也是有用的思维工具,可以通过顶点和边的表示来解决问题。
五、BMO竞赛奖项设置
Round 1
铜奖:英国Top51-100
优秀奖:约Top15%的学生获得
荣誉奖(Merit):约TOP 45% 的学生获得
*中国的参赛者将根据英国的截止分数进行评判
Round 2
区别奖:BMO Round 1 成绩排名前 10% 的学生才有资格参加 Round 2
六、BMO竞赛含金量优势
1. 升学背景提升
进入顶尖大学的金钥匙:BMO由UKMT主办,其第一轮(BMO1)相当于美国数学邀请赛(AIME)。高含金量使其成为申请牛津、剑桥等G5大学的有力支撑。在标化成绩(如A-level成绩)无法明显拉开差距的情况下,BMO成绩成为申请者脱颖而出的好方法。取得BMO好成绩,相当于提前打开了知名大学的录取通道。
2. 学术能力证明
高水平数学能力的象征:BMO是UKMT系列中级别最高的赛事,题目难度大,深入考察数学能力和逻辑推理技巧。在BMO中获奖能够充分证明个人的数学学术能力,显示出对复杂问题的理解和解决能力。
3. 反哺国际课程的数学学习
提高国际课程中的数学成绩:通过BMO的学习和思考,学生可以培养对数学的钻研兴趣,提前深入了解数学专业及题目背后的背景知识。这种深入学习能够反哺A-Level、IB、AP等国际课程中的数学科目学习,提升整体学术水平。
七、BMO竞赛备考建议
1. 4-7月:串联知识点
系统化学习
在这一阶段,重点是系统化地串联和复习数学知识点。BMO的试题强调数学能力和逻辑推理技巧,要求学生用数学推理解决有趣的问题。因此,同学们需要有意识地将各个知识点串联起来,尤其是BMO真题中那些高频考点。
分类题目练习
基于知识点进行分类题目练习,确保对每个知识点的掌握。在这一过程中,尽可能地拓展自己的知识面,练习更多不同类型的题目,甚至是其他数学竞赛的题目,以提升整体数学水平。
强化理解与应用
注重理解知识点背后的数学原理,培养将这些知识点应用于不同问题中的能力。这种深入的理解和广泛的应用将为后续的解题打下坚实基础。
2. 8-11月:学习解题思路
培养解题思维逻辑
BMO以证明题为主,对过程和步骤有严格要求,需要培养解题思维逻辑和表达能力。在刷题过程中,要着重观察每一道题的解题逻辑和标准答案的解题步骤。
刷题与分析
反复刷真题,深入分析真题的解题方法。从真题中找到解题的逻辑和思路,持续提高自己的解题能力和水平。做完真题后,注重总结和归纳,整理出自己的错题集,反复进行思考。
标准解题步骤
学习如何书写规范的证明过程。BMO注重逻辑性和严谨性,因此在解题过程中,要注意书写清晰、条理分明的解题步骤,确保每一步都有逻辑支持。
