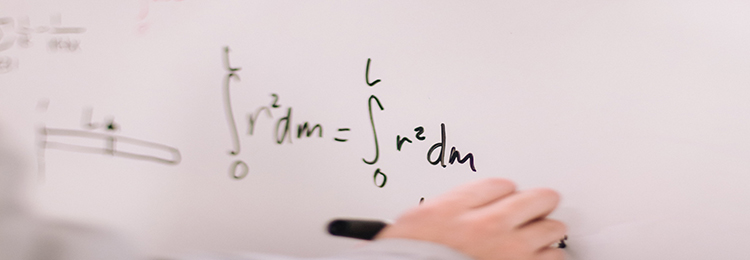BMO数学奥赛考试核心内容

英国数学奥林匹克竞赛（BMO）以证明题为载体，构建了涵盖数论、几何、代数与组合数学的四大核心知识体系。本文系统解析竞赛知识权重分布、题型难度梯度、命题趋势演变及策略性备考路径，揭示其作为IMO英国国家队选拔核心机制的评价逻辑与学术价值。

一、竞赛定位与核心价值

双轮进阶机制

Round 1：6道证明题，限时3.5小时，满分60分。全球前10%选手晋级（约100人）。

Round 2：4道高阶证明题，满分40分，优胜者进入英国IMO国家队集训营。

语言壁垒：全英文题干含500+专业术语（如"modular arithmetic"），需突破学术阅读障碍。

学术能力认证

牛剑录取关联：牛津、剑桥数学系录取者中近40%拥有BMO奖项，解题逻辑常成为面试核心素材。

课程衔接价值：覆盖A-Level进阶数学（Further Maths）70%核心模块，强化多项式理论、矩阵变换等大学先修内容。

二、知识版图深度解析

四大领域权重分布

知识模块	占比	核心考点	典型题型
数论	30%-40%	质因数分解、同余方程、费马小定理	求正整数解满足 $n^{2} + 20 n + 11 = k^{2}$ （需模4分析）
几何	25%-30%	圆幂定理、三角形四心性质、复数几何旋转	向量点积证三维空间垂直性/海伦公式算复合图形面积
代数	20%-25%	柯西-施瓦茨不等式、递归关系、生成函数	证明 $a + b a ^{2} + b ^{2} + b + c b ^{2} + c ^{2} + c + a c ^{2} + a ^{2} \geq a + b + c$
组合数学	15%-20%	鸽巢原理、图论基础、递推关系	证任意10个实数中存在两数使 $a + b$ 与 $ab$ 非负

跨学科融合新方向

环境科学建模：碳交易市场博弈策略的数学优化。

密码学应用：RSA加密算法中的大数分解与欧拉定理验证。

三、题型结构与难度梯度

Round 1 命题特征

基础题（第1-2题）：概念辨析为主，如名义利率与实际利率计算，但设置干扰条件。

中档题（第3-4题）：多步骤复合推理，例如先求导分析函数极值，再结合柯西不等式放缩。

高难题（第5-6题）：开放型问题，如设计发展中国家产业升级路径的数学模型。

Round 2 难度跃升点

逻辑链延长：需连续4-5步推导（例：质因数分解→构造同余方程→验证解合理性）。

工具深化：动态规划解资源分配问题，或微积分计算旋转体体积。

四、命题趋势与能力要求

三大演变方向

现实问题抽象化

2024年真题引入城市交通网络最短路径优化，需结合图论与极端原理。

计算工具整合

允许使用编程辅助验证（如Python实现质数筛法），但需书面推导过程。

证明严谨性升级

步骤缺失直接导致分值折损（如未标注Hammett方程适用条件扣30%分数）。

能力评价维度

维度	权重	评价标准
知识迁移	40%	大学数学理论的应用准确性（如群论证对称性）
逻辑完备性	30%	推导过程无断链，反证法/归纳法使用规范
计算精确度	20%	结果保留三位有效数字，量纲完整
模型创新	10%	对开放问题提出可验证解法（如CO₂捕集工艺）

五、备赛策略框架

三阶段能力建构模型

阶段	时间窗	训练重点
知识重构	6月-9月	突破数论（同余方程）与几何（复数旋转）
真题淬炼	9月-10月	精练2019-2024真题，建立红标错题本（重点标注逻辑漏洞）
极限模拟	11月考前	全真限时训练（前两题≤40分钟）+ 压轴题特训

高频失误防控指南

单位换算陷阱：范德华气体方程中温度单位未统一（K与℃混淆）。

边界条件遗漏：同余方程解集未验证整数范围导致漏解。

压轴题策略：第6题平均正确率＜5%，建议确保前4题满分后再攻关。

BMO通过四大知识模块的深度整合与证明题型的严谨架构，成为检验数学思维纯度的试金石。参赛者需把握“数论几何优先突破”“逻辑链零容错”“开放题建模意识”三大原则，在抽象理论与现实应用的辩证中完成思维跃迁。建议以组合数学中的递推关系与几何复数变换为突破口，通过跨学科问题重构知识网络，最终实现竞赛能力与学术素养的双重进化。